Применение волнового алгоритма для нахождения скелета растрового изображения.

1. Бинарное растровое изображение

Под бинарным растровым изображением будем понимать двумерную матрицу из черных и белых точек, в которой объект задается черными точками растра, а фон – белыми точками.

С точки зрения анализа растрового изображения введем следующие определения:

• отрезок изображения
• соединение отрезков
• пересечение отрезков

Под изображением линии (отрезком) на растре будем понимать такое множество черных точек растра, что можно провести отрезок прямой AB такой, что по обе стороны от этого отрезка будет лежать примерно равное количество точек, и расстояния от отрезка до ближайших крайних точек изображения будут отличаться не более чем на наперед заданную величину (Рисунок 1а).

Под соединением отрезков будем понимать два отрезка такие, что одна из вершин одного отрезка лежит на другом отрезке. В этом случае они будут иметь одну общую точку и один из отрезков будет разделен на два. (Рисунок 1б).

Пересекающиеся отрезки изображения будем представлять в виде отрезков меньшей длины, имеющих одну общую вершину (Рисунок 1в).

а	б	в
Рисунок 1

2. Векторное представление в виде нагруженного графа

Под векторным представлением растрового изображения будем понимать такой нагруженный граф, у которого нагрузка вершин – пары координат x,y соответствующих узловых точек изображения.

За узловые точки будем принимать точки соединения изображения линий в растровом изображении. Толщиной линии будем считать ее ширину в пикселях.

В зависимости от выбираемой стратегии изображение может рассматриваться как состоящее из отрезков прямой (Рисунок 2а) , либо включающее дуги (Рисунок 2б). Переход от первого представления ко второму возможен путем нахождения такой последовательностей ребер, которая наиболее полно приближается по начертанию к дуге. Для этого необходимо просматривать все последовательности из 3 и более ребер, анализируя взаимное расположение отрезков прямой. От выбора стратегии анализа взаиморасположения отрезков будет зависеть точность представления.

а	б
Рисунок 2

Граф для представления остова изображенной на Рисунок 2б буквы P представлен на Рисунок 3, а соответствующие матрицы нагрузок и инцидентности в Таблица 1: Нагрузки вершин и ребер: и Таблица 2: Матрица инцидентности графа: соответственно.

Рисунок 3

Как видно, по графу возможно восстановить исходное растровое изображение. Для этого необходимо произвести отрисовку ребер графа согласно нагрузкам вершин и матрице инцидентности.

3. Волновой метод отслеживания центральной линии и соединений отрезков

Метод заключается в анализе пути прохождения сферической волны по изображению. На каждом шаге анализируется смещение центра масс точек, образующих новый шаг (генерацию) волны, относительно его предыдущих положений.

Метод состоит из следующих шагов:

1. Построение скелета изображения с помощью сферической волны
2. Оптимизация полученного скелета

До построения скелета, с целью улучшения качества изображения возможно применение различных фильтров. В частности, желательно избавить изображение от случайного шума.

Волновые алгоритмы часто используются в компьютерных играх для определения минимального расстояния от одного объекта до другого в ограниченном дискретном пространстве. Для этого, в исходной точке генерируется волна, распространяющаяся по определенным законам, помечающая пройденные точки номером шага. Процесс заканчивается по достижении целевой точки. Номер шага, которым помечена целевая точка и будет расстоянием от исходной до целевой точки.

При распространении волны на растре мы сталкиваемся со следующими ограничениями [1]:

• дискретность пространства
• дискретность направлений распространения (90 градусов для 4-х связного растра, 45% для 8-и связного растра)

С учетом этих ограничений, законы распространения волн будут отличаться для 4-х связного растра (Рисунок 4а), 8-ми связного растра (Рисунок 4б). Также допустимы более сложные законы распространения. При 4-х связном растре распространение идет в форме ромба, при 8-связном – в виде квадрата.

Для генерации сферической волны необходимо скомбинировать 4-х и 8-и связное распространение волны Рисунок 4в). Это достигается попеременным применением 4-х и 8-и связного распространения. В результате получаем распространение в виде восьмиугольника прекрасно огибающего препятствия.

а	б	в
Рисунок 4

3.1.1 Распространение волны на отрезке прямой

При распространении сферической волны на отрезке прямой наблюдаются следующие эффекты: не более чем через 2*N шагов распространение волны приобретает устойчивый характер вне зависимости от начальной точки распространения волны (см. Рисунок 5). Причем N – ширина линии в пикселях.

а	б	в
Рисунок 5

3.1.2 Распространение волны на кривой

При отличии формы отрезка от прямой, распространение волны также предсказуемо, причем необходимо отметить хорошие огибающие свойства сферической волны (см. Рисунок 6)

а	б	в
Рисунок 6

3.1.3 Огибание препятствий волной

Если на пути распространения волны встречаются препятствия, то поведение волны целиком зависит от формы и размеров препятствий. Мелкие препятствия (1-2 пикселя) мало влияют на распространение волны, внося незначительные помехи (Рисунок 7а). Более крупные помехи на изображении вызывают значительные искажения картины распространения волны (Рисунок 7б).

а	б
Рисунок 7

Однако возможно удаление мелких помех до применения метода скелетизации (различные фильтры изображения [4]). Средние и крупные помехи на изображении будут причинять неудобство и для других конкурентных методов векторизации. Кроме того, в большинстве случаев, крупные помехи являются элементами изображения.

3.1.4 Разделение волны на пересечении отрезков

При достижении волной места соединения двух или более отрезков наблюдается разделение волны на несколько дочерних волн, сохраняющих поведение материнской волны (рис. Рисунок 8). Момент разделения довольно просто отслеживается путем анализа “ширины” волн, т.е. количества точек образующих очередную генерацию волны: перед разделением наблюдается увеличение “ширины” волны с дальнейшим разделением волны на две (иногда более) дочерние волны.

а	б	в
Рисунок 8

3.2 Отслеживание формы объекта с помощью сферической волны

3.2.2 Отслеживание линий изображения

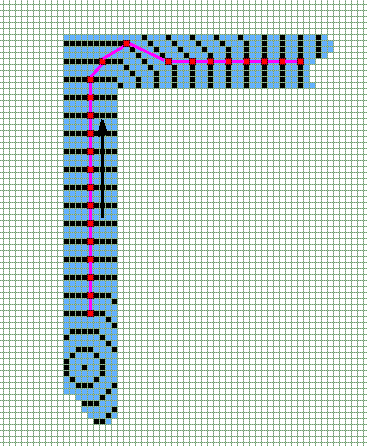
Отслеживание отрезков производится путем отслеживания перемещения центра отрезка, образуемого крайними точками генерации волны (Рисунок 9а). После отслеживания возможно сглаживание отрезков (с целью сокращения узловых точек).

Если отслеживаемая линия не является прямой, то получается не одна линия, а множество отрезков, интерполирующих исходный рисунок (Рисунок 9б).

а	б
Рисунок 9

3.2.2 Определение места соединения отрезков

Выявление мест увеличения “ширины” волны и разделения волны на дочерние позволяет установить точку предполагаемого соединения двух отрезков. Определение увеличения “ширины” волны производится путем сравнения “ширины” очередной генерации волны и ее среднего значения за N предыдущих генераций (N задается заранее). Причем мы получаем 2 крайние точки (A,B) трассируемого отрезка. После разделения волны на 2 полуволны, мы получаем еще 2 пары точек (C,D) и (E,F).

С помощью анализа этих отрезков (AB, CD, EF) можно оценить положение точки соединения отрезков.

Всего, обобщенно, возможно 6 вариантов прохождения волной места соединения отрезков (Рисунок 10). В любом из возможных вариантов точка соединения отрезков лежит внутри шестиугольника ABCDEF. Первоначально установим место соединения как центр масс этого многоугольника. Коррекция будет возложена на оптимизацию скелета изображения.

а	б	в
г	д	е
Рисунок 10

3.3 Оптимизация полученного скелета

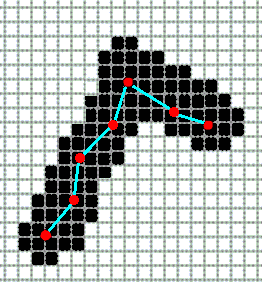
Полученный скелет изображения не является оптимальным. Это связано прежде всего с тем, что мы имеем дело с растровым изображением, а значит, изображение имеет искажения тем большие, чем меньше размер изображения в пикселях. (Рисунок 11)Качество исходного материала, который был подвергнут оцифровке с целью ввода в ЭВМ, также сильно проявляет себя в виде дефектов изображения.

а	б
Рисунок 11

Для уменьшения влияния искажений на получаемый скелет необходимо произвести оптимизацию скелета, полученного отслеживанием пути сферической волны по изображению объекта. В получаемом скелете возможно представление одного отрезка некоторой последовательностью ребер (Рисунок 12а). Избиться от этого можно анализом последовательности ребер, оценивая отклонение получающейся линии от прямой. В случае, если отклонение находится в допустимых пределах, необходимо в скелете заменить соответствующую последовательность ребер на одно, возможно с модификацией его концевых точек (Рисунок 12б).

а	б
Рисунок 12

3.3.1 Оптимизация отрезков

Искажения, вызванные низким разрешением изображения (Рисунок 13а) удаляются путем анализа последовательности ребер. При этом точки, образующие последовательность ребер, должны отклоняться от коррелирующей прямой не больше, чем на заранее заданную величину, соизмеримую с шириной линии. От задаваемой величины зависит качество оптимизации: чем больше допустимое отклонение, тем меньше точек будет входить в результирующий граф. (Рисунок 13б,в).

а	б	в
Рисунок 13

3.3.2 Оптимизация точки соединения отрезков

Для оптимизации скелета просматриваются окрестности выделенных точек соединения отрезков, т.е. таких точек, где наблюдается разделение волны на полуволны.

Наиболее часто встречающиеся искажения (Рисунок 14а) исправляются с помощью анализа прилежащих к выделенной точке (А) отрезков (AB₁, B₁C₁, AB₂, B₂C₂, AB₃, B₃C₃). Анализ заключается в поиске такой пары отрезков C_xB_x, B_yC_y из (B₁C₁, B₂C₂, B₃C₃), что C_xB_xB_yC_y максимально коррелируются прямой. Тогда необходимо точку A переместить в точку пересечения прямых C_xC_y и AС₂, а затем удалить из графа точки B₁, B₂ и B₃ (Рисунок 14б).

а	б
в	г
Рисунок 14

Другим вариантом искажения является случай соединения трех отрезков в одной точке (Рисунок 14в). В этом случае невозможно нахождение пары отрезков коррелируемых прямой. Точка A должна быть перемещена в центр треугольника образуемого прямыми B₁C₁, B₂C₂ и B₃C₃. Затем точки B₁, B₂ и B₃ необходимо удалить из графа (Рисунок 14г).

3.4 Алгоритм построения скелета изображения с помощью сферической волны

Построение скелета сводится к выделению отрезков и мест их соединения с занесением найденных данных в результирующий граф. Выделение производится с помощью анализа пути прохождения волны, с пометкой пройденного пути (для предотвращения двойного прохождения волны по изображению).

В результирующий граф скелета изображения заносятся средние точки для каждой генерации волны. уменьшения количества точек в процессе движения волны производится анализ перемещения средней точки последней генерации волны, и в граф заносятся только точки, в которых происходит изменение направления движения средней точки (Рисунок 15а).

Для выделения ребер определяются точки где:

1. происходит разделение волны на полуволны, т.е. соединение или пересечение отрезков (Рисунок 15б)
2. происходит затухание волны, т.е. конец отрезка (Рисунок 15в)

В случае затухания волны возможны два варианта:

1. мы нашли конец ребра (Рисунок 15в)
2. мы нашли точку соединения ребер (Рисунок 15г)

Алгоритм поиска скелета является рекурсивным. Для организации рекурсии используется стек для хранения генераций волн. Поиск оканчивается, когда весь объект становится помеченным (то есть нет возможности для дальнейшего распространения волны).

а	б
г	д
Рисунок 15

Алгоритм:

1. создаем пустой стек для хранения генераций волны
2. заносим в него любую точку изображения как генерацию волны
3. пока стек не пуст продолжаем шаги 4-8
4. выбираем генерацию волны из стека
5. продолжаем волну из выбранной точки изображения, пока не произойдет разделение волны на полуволны или затухание волны
6. если произошло затухание волны, то пройденный путь является кривой, заносимой в граф (возможно замкнутой, если затухание волны произошло на границе с помеченной волной областью); переходим к п. 3
7. если волна разделилась на полуволны, то мы нашли место соединения двух отрезков и в граф заносится пройденный путь. В стек заносим обе полуволны
8. переходим к п. 3

3.5 Алгоритм оптимизации скелета

Для оптимизации скелета необходимо выделить все последовательности ребер такие, что отклонения от коррелирующей прямой для них будет минимальным и выправления положения точки пересечения отрезков.

Алгоритм оптимизации скелета:

1. первичная оптимизация точек соединения отрезков
2. оптимизация ребер скелета
3. вторичная оптимизация точек соединения отрезков

Нахождение последовательности ребер производится последовательным дополнением списка ребер ребрами инцидентными крайним ребрам последовательности. Оптимизированные ребра помечаются. Невозможна оптимизация последовательности ребер, если одна из внутренних точек последовательности имеет степень больше 2.

Алгоритм оптимизации ребер скелета:

1. Пока есть непомеченные ребра выполняем п. 2- 9.
2. Очистить последовательность ребер.
3. Добавить в последовательность непомеченное ребро.
4. Найти непомеченное ребро, инцидентное последовательности ребер, проверив требования к степеням вершин, входящих в последовательность.
5. Если таких ребер нет – перейти к п. 8.
6. Занести найденное ребро в последовательность
7. Если для последовательности ребер невозможно провести коррелирующую прямую, то удалить ребро добавленное в п. 6.
8. Перейти к п. 4.
9. Заменить в графе полученную последовательности ребер одним ребром, пометив его.

После оптимизации ребер необходимо произвести оптимизацию точек соединения ребер. Это делается в два прохода: первый выполняется до оптимизации ребер, второй после.

Алгоритм первичной оптимизации точек соединения ребер:

1. Пока есть непомеченные вершины со степенью 3 выполняем 2-7
2. Выбрать очередную вершину
3. Найти пару ребер C_xB_x, B_yC_y такую, что образуемые ими прямые образуют угол в 180±N градусов (N задается заранее).
4. Если такую пару ребер найти невозможно, то перемещаем вершину в центр треугольника, образуемого прямыми B₁C₁, B₂C₂ и B₃C₃
5. Иначе, оптимизируем вершину, помещая ее в точку пересечения прямых C_xC_y и AC₂
6. Удаляем из графа вершины B₁, B₂, B₃, соединяя вершины C₁, C₂, C₃ с вершиной A
7. Помечаем оптимизированную вершину

Алгоритм вторичной оптимизации точек соединения ребер:

1. Пока есть непомеченные вершины со степенью от 3 до 5 выполняем 2-7
2. Выбрать очередную вершину
3. Для ребер, инцидентных данной вершине A, найти пару ребер AB,AC такую, что они образуют угол в 180±N градусов (N задается заранее).
4. Если такую пару ребер найти невозможно, то такая вершина не нуждается в оптимизации; помечаем вершину и переходим к п. 2
5. Если степень вершины = 3, то оптимизируем вершину, помещая ее в точку пересечения прямой BC и АD
6. Если степень вершины = 4, то помещаем вершину в середину отрезка FG, где точка F получается пересечением прямых BC и AD, а точка G пересечением прямых BC AE.
7. Помечаем оптимизированную вершину

4 Заключение

В статье рассмотрен новый метод получения скелета растрового изображения. Предлагаемый метод является эффективным с точки зрения точности получаемого скелета.

Преимущества:

1. процесс скелетизации происходит на том же изображении, что позволяет добиться экономии памяти
2. память используется для создания стеков при организации генерации волны и запоминания пройденного пути
3. генерация волны происходит в пространстве N², что не требует использования операций над действительными числами
4. Количество операций прямо пропорционально заполнению (площади скелетизируемого объекта)

Таким образом, представленный алгоритм может с успехом использоваться при создании программ распознавания текста, конструкторской документации, в ГИС и САПР.

Литература:

1. Е.В. Шикин, А.В. Боресков Компьютерная графика. “Мир”, Москва, 1995.
2. Л.М. Местецкий Непрерывный скелет бинарного изображения. Доклад на конференции Графикон-99
3. И. Денисов, Е. Кузьмин Эффективный алгоритм построения остова растрового изображения. Доклад на конференции Графикон-99
4. Е.А. Бутаков, В.И. Островский, И.Л. Фадеев Обработка изображений на ЭВМ. Москва, “Радио и связь”, 1987
5. Ф. Препарата, М. Шеймос Вычислительная геометрия: Введение. Москва, “Мир”, 1989
6. Л.Т. Кузин Основы кибернетики, Т.2 Москва, “Энергия”, 1979

http://ocrai.narod.ru E-Mail: ocrai@narod.ru последнее обновление: 03;05;2001